非線形次元削減の概要
カリフォルニア工科大学のYoutube動画「非線形次元削減の概要」について要点と要約をまとめました

3つの要点
- 要点1
線形次元削減は有用だが、データの非線形構造を十分に表現できない場合がある - 要点2
非線形次元削減は、線形部分空間が十分でない場合やデータの固有次元が低い場合に有益 - 要点3
KPCAはデータを高次元の特徴空間にマッピングし、主成分分析を行う手法である

要約
非線形次元削減の導入
この講義では、デビッド・トンプソンが非線形次元削減の概念を紹介し、線形射影からの脱却を説明しています。彼は、線形部分空間は一般的に有用であるが、データの基礎的な多様体を十分に表現できない場合があると述べています。非線形次元削減は、データの非線形構造を捉えることでより効率的な表現を見つけることを目指しています。
非線形次元削減の利点と落とし穴
トンプソンは、線形手法と比較して非線形手法の利点と落とし穴を強調しています。非線形次元削減は、線形部分空間が十分でない場合やデータの固有次元が低い場合に有益ですが、より多くのデータが必要であり、退化した解や不安定性を引き起こす可能性があります。トンプソンは、非線形手法に頼る前に線形次元削減戦略から始めることを勧めています。
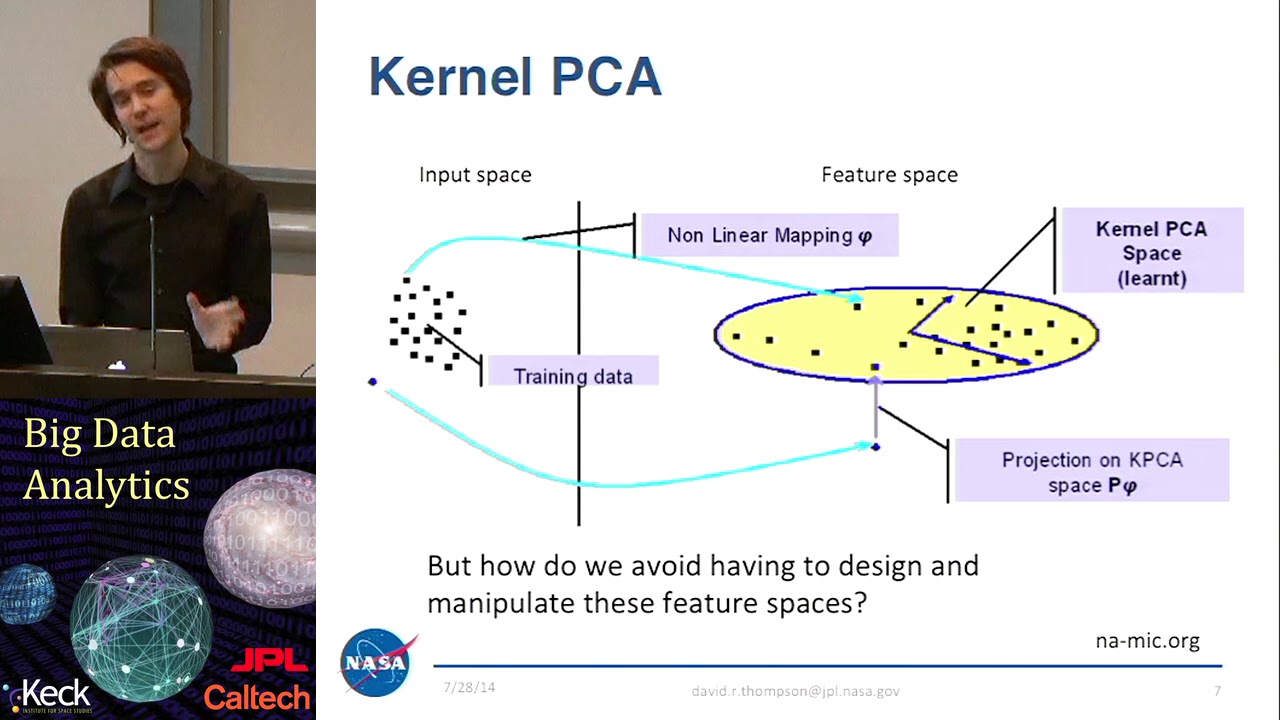
カーネル主成分分析(KPCA)
トンプソンは、広く使用されている非線形次元削減手法であるカーネル主成分分析(KPCA)に焦点を当てています。彼は、KPCAがデータをより高次元の特徴空間にマッピングし、その空間で主成分分析を行うことを説明しています。トレーニングデータから学習した射影は、新しいデータポイントを高次元の特徴空間に射影するために使用することができます。
実際の考慮事項と他の非線形次元削減手法
トンプソンは、KPCAの実装における実際的な考慮事項について議論しています。カーネル関数の選択や高次元特徴空間でのデータの中心化など、KPCAの実装における実践的な考慮事項について触れています。彼はまた、ラプラシアン固有値など、他の非線形次元削減手法についても言及しています。
▼今回の動画
編集後記
▼ライターの学び
非線形次元削減は、データの非線形構造を捉えるために有用であることを学びました。また、線形次元削減戦略から始めることが重要であることも理解しました。

▼今日からやってみよう
今日から線形次元削減手法を試してみて、データの非線形構造をより効率的に捉えるための非線形次元削減手法に移行することができます。








