サブサンプリングとサンプリング分布の推定における重要性の紹介
カリフォルニア工科大学のYoutube動画「サブサンプリングとサンプリング分布の推定における重要性の紹介」について要点と要約をまとめました

3つの要点
- 要点1
サブサンプリングは、ブートストラップ法が効果的でない場合に有用です。 - 要点2
サブサンプリングは、サンプル自体をランダムに扱い、確率的な記述を行うことができます。 - 要点3
サブサンプリングは、定常m-従属系列や極端な場合に特に有用です。

要約
サブサンプリングの導入
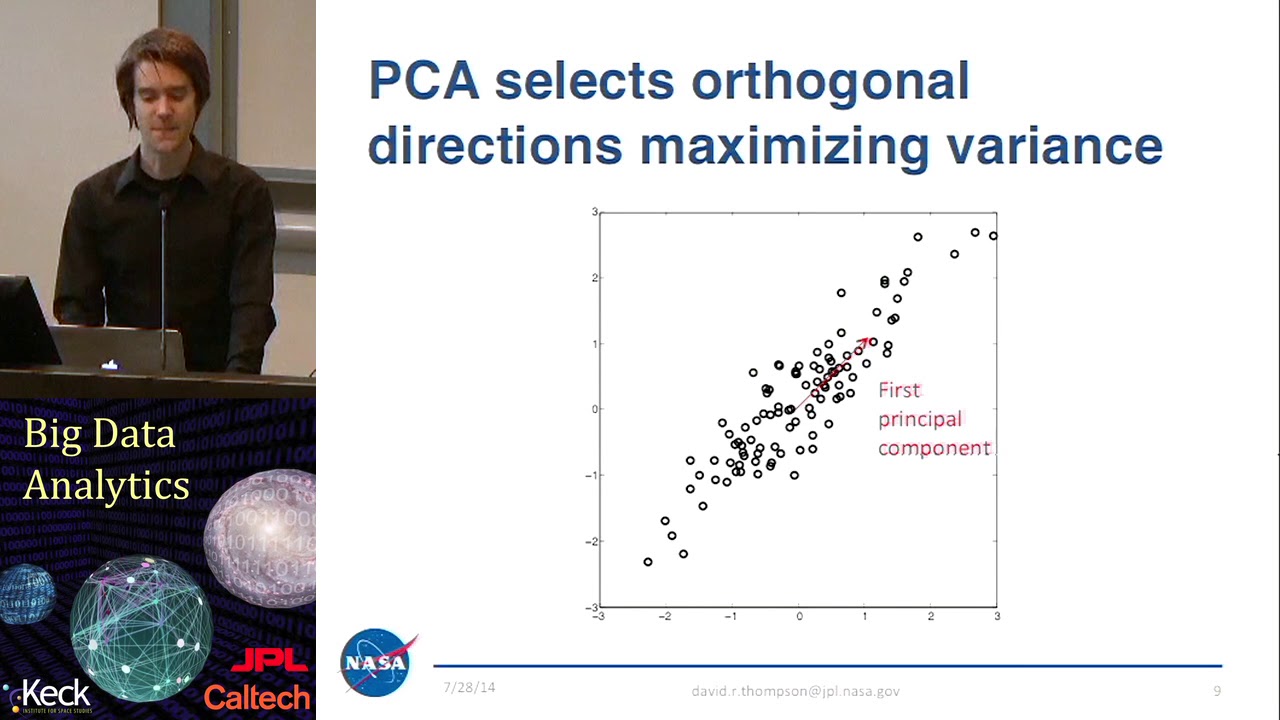
このJPL Caltech仮想サマースクールの最終モジュールでは、サブサンプリングの技術を紹介します。サブサンプリングは、確率分布が不明な場合に統計量のサンプリング分布を推定するための非パラメトリックな方法です。この方法は、ブートストラップ法が効果的でない場合に特に有用です。このセクションの資料は、Das Gupta教授とCharlie Dyer教授から提供されたノート、およびPolitis、Romano、Wolfeによる書籍「サブサンプリング」に基づいています。
リサンプリングとサブサンプリングの違い
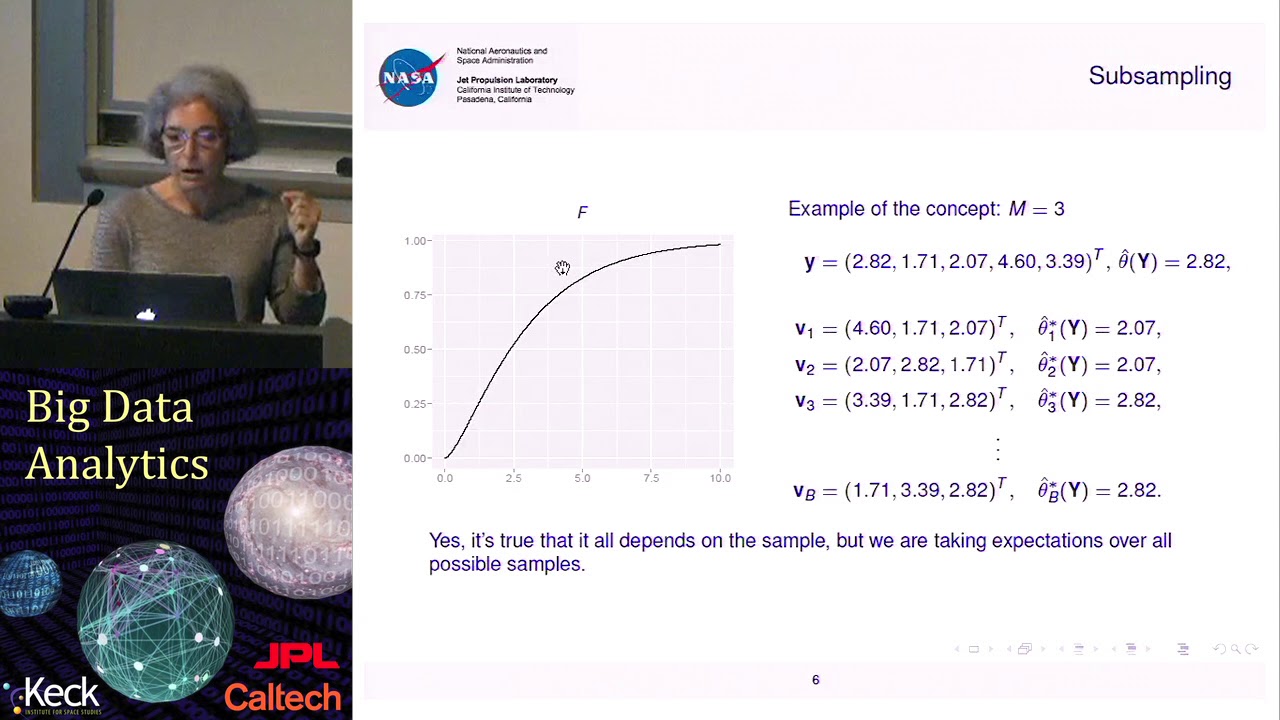
ブートストラップ法では、元のサンプルから置換を用いて再サンプリングを行います。しかし、サブサンプリングでは、元のサンプルから置換を用いずにサブサンプルを抽出します。これはつまり、サブサンプリングは真の分布から抽出し、リサンプリングはサンプルの経験的分布から抽出するということです。その主な違いは、サブサンプリングはサンプル自体をランダムに扱うため、すべての可能なサンプルに対して確率的な記述を行うことができるということです。これらのサブサンプルは、興味のある統計量の推定値を計算するために使用され、これらの推定値の分布はモンテカルロ法を用いて近似することができます。
サブサンプリングの条件と利点
サブサンプリングは効果的に機能するためには、2つの比較的弱い条件が必要です。それは、統計量の中心化およびスケーリングバージョンの収束性、およびスケーリング指数の存在です。これらの条件が満たされると、サンプルサイズが増加するにつれて、サブサンプリング分布関数は真の分布関数に収束します。サブサンプリングは、定常m-従属系列や極端な場合に特に有用であり、ブートストラップ法がうまく機能しない場合があります。ただし、サブサンプルサイズmの選択は重要であり、いくつかの実験が必要な場合があります。
考慮事項と結論
サブサンプリングとブートストラップ法の選択は、問題自体とバイアスと分散のトレードオフに依存します。サブサンプリングはバイアスを減らすことができますが、分散を増加させる可能性があります。一方、ブートストラップ法は逆の効果を持つかもしれません。これらの方法は漸近的な保証を提供し、常に真であるとは限らない仮定に依存しています。したがって、実験と感度分析を実施し、異なる仮定がデータから引き出される結論に与える影響を評価することが推奨されています。全体的に、サブサンプリングとブートストラップは現代のデータ分析において貴重な技術ですが、政策決定において結果を解釈する際には注意が必要です。
▼今回の動画
編集後記
▼ライターの学び
サブサンプリングとブートストラップ法の違いや条件、利点について学びました。

▼今日からやってみよう
今日からデータ分析においてサブサンプリングやブートストラップ法を適用してみましょう。