2023.12.14

デジタル関数とフーリエ変換の理解

marugotoyoten

カリフォルニア工科大学のYoutube動画「デジタル関数とフーリエ変換の理解」について要点と要約をまとめました

３つの要点

要点１
デジタル関数はピクセルで表現され、そのフーリエ変換は正弦波の振幅と位相で構成されています。
要点２
フーリエ変換は元の関数を正弦波、振幅、位相で表現し、元の関数と相互変換可能です。
要点３
異なる1次元関数には異なるフーリエ変換があり、フーリエ変換は元の関数の成分を逆空間で分離します。

要約

デジタル関数とその表現についての導入
構造生物学では、連続関数ではなくデジタル関数を使用することがよくあります。デジタル関数はピクセルで表現され、各ピクセルでアナログ信号をサンプリングしてデジタル画像を作成します。デジタル画像のフーリエ変換は、元の関数を再現するために必要な正弦波の振幅と位相で構成されています。

フーリエ変換の構成要素
デジタル画像のフーリエ変換は、いくつかの要素で構成されています。最初の要素はDC成分であり、画像全体の関数の平均値を表します。次の要素は基本周波数とその位相であり、その後に高調波とその位相が続きます。最後の要素はナイキスト周波数であり、画像に存在する最高周波数成分を表します。

元の関数とそのフーリエ変換の相互変換性
元の関数とそのフーリエ変換は同じ関数の異なる表現です。フーリエ変換は正弦波、振幅、位相を用いて関数を表現し、元の関数は位置の関数として密度を表現します。これらの2つの表現は相互に変換可能であり、元の関数からフーリエ変換を計算したり、逆にフーリエ変換から元の関数を計算したりすることができます。

1次元関数とそのフーリエ変換の例
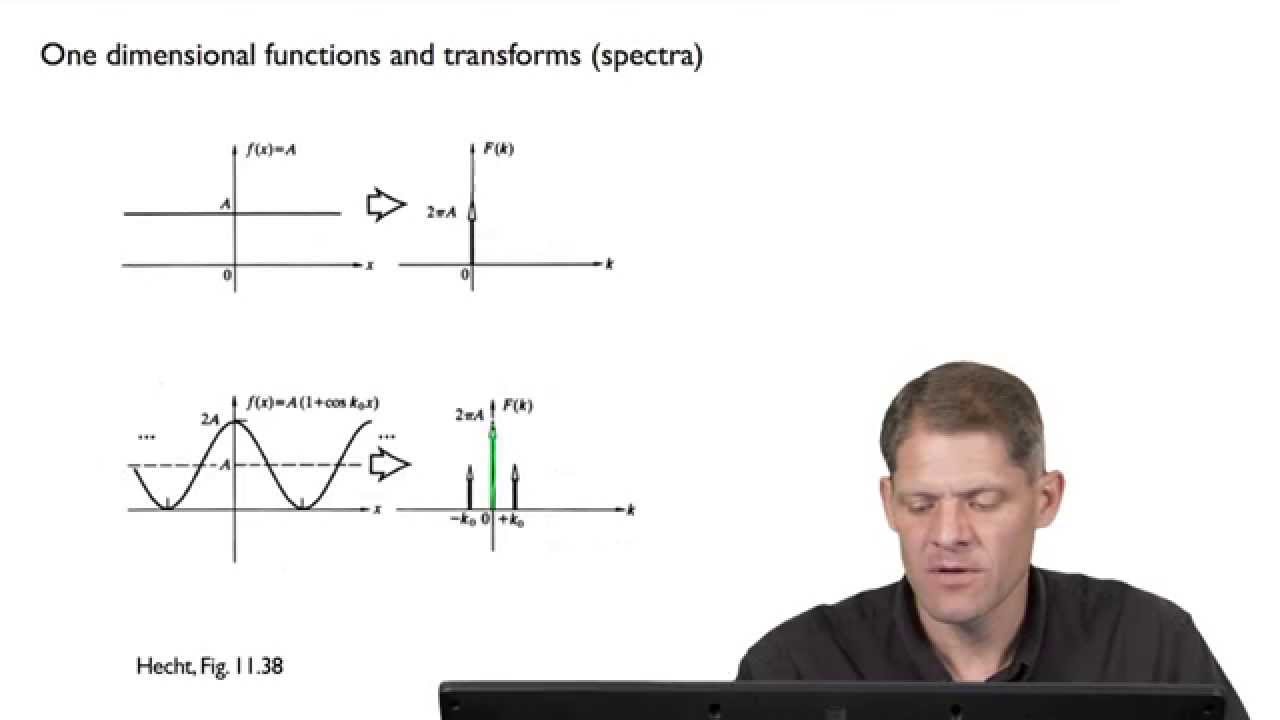
異なる1次元関数には異なるフーリエ変換があります。例えば、コサイン関数には周波数とその負の周波数の1つの成分があります。定数関数にはゼロ空間周波数で1つの成分があります。平均値がゼロでない関数にはゼロ空間周波数での成分とその周波数での成分があります。フーリエ変換はこれらの成分を分離し、逆空間で表示します。

▼今回の動画