次元削減と線形手法の紹介
カリフォルニア工科大学のYoutube動画「次元削減と線形手法の紹介」について要点と要約をまとめました

3つの要点
- 要点1
次元削減とは、データをより低次元の空間に射影することで、データの視覚化や分析を容易にする手法です。 - 要点2
次元削減は、実際のプロセスが低次元の構造を持つことが多いという直感に基づいています。冗長な次元を削減することで、データセットの情報を保持しながら、より効率的に処理することができます。 - 要点3
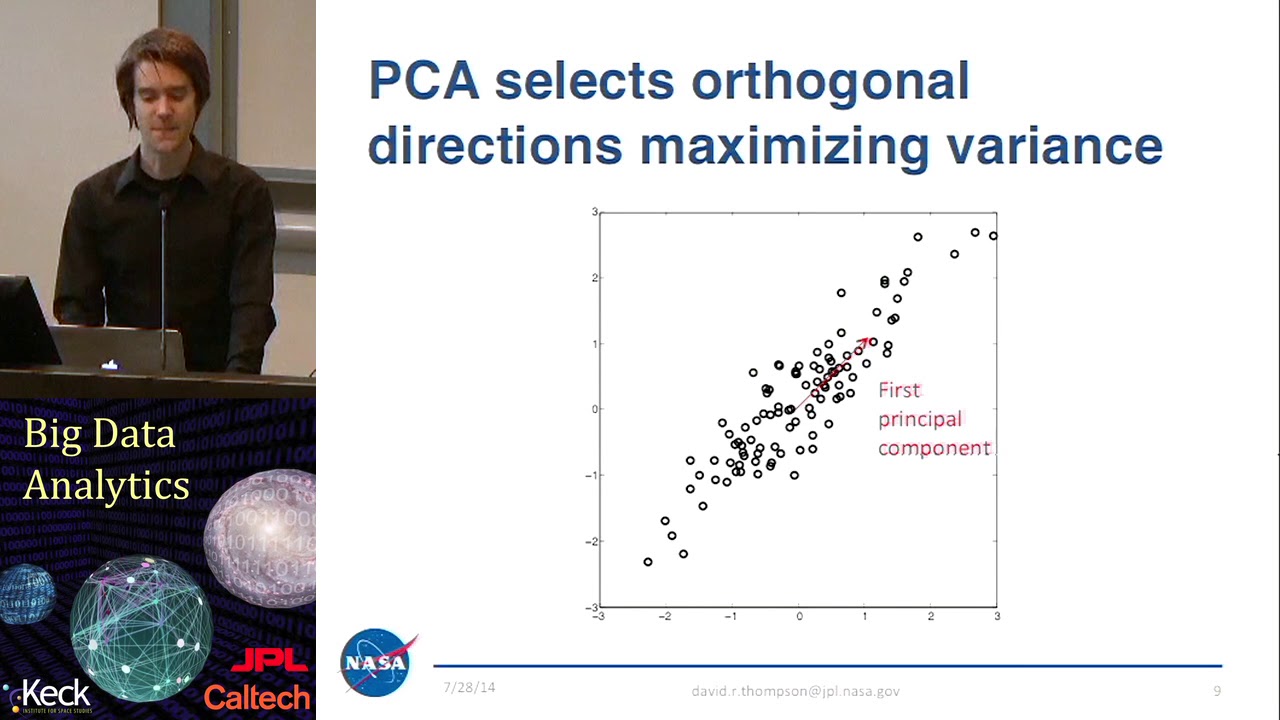
PCAは、データセットの分散を最大化する直交方向を特定する手法です。固有顔は、PCAの具体的な応用例であり、顔認識や検出に使用されます。

要約
次元削減と特徴選択の関係について
この講義では、私、デイビッド・トンプソンが次元削減とその特徴選択との関係について説明します。特に、主成分分析(PCA)とその特異値分解との関係に焦点を当てます。目的は、データの興味深い射影を見つけることで、すべての属性を利用しながら、より低次元の空間でデータを視覚化および分析しやすくすることです。
次元削減の直感と目的
次元削減は、実際のプロセスが高次元の属性空間に埋め込まれた低次元の構造を持つことが多いという直感に基づいています。目標は、この低次元の多様体または部分空間を明らかにすることです。冗長な次元を削減することにより、データセットのすべての情報を保持する低次元の射影を見つけることができます。画像解析は、サムネイル画像などの高次元データを効果的に低次元の多様体に削減することができる分野の一つです。
主成分分析(PCA)と固有顔
PCAは、次元削減に使用される一般的な線形手法です。データセットの分散を最大化する直交方向を特定します。これらの方向は、データの異なる変動軸として解釈することができます。固有顔は、PCAの典型的な例であり、顔認識や検出に広く使用されています。固有系に関連する固有値は、データセットの固有次元性についての洞察を提供します。
効率的な実装と結論
大規模なデータセットにおいては、PCAの効率的な実装が重要です。特異値分解は、主成分を計算するための代替手法として使用することができます。他のアプローチには、一度に1つの主成分を計算する方法やオンライン学習戦略を使用する方法があります。まとめると、PCAは信頼性の高い有用な次元削減および視覚化ツールです。データセットの構造に関する貴重な洞察を提供し、幅広いパターン認識の問題に適用することができます。
▼今回の動画
編集後記
▼ライターの学び
次元削減は、データの視覚化や分析を容易にするための重要な手法であり、実際のプロセスには低次元の構造が埋め込まれていることが多いということを学びました。

▼今日からやってみよう
今日から、自分のデータセットに対してPCAを適用して、データの構造を視覚化し、洞察を得ることができます。