2023.12.14

ブラウン運動の紹介と特性

marugotoyoten

カリフォルニア工科大学のYoutube動画「ブラウン運動の紹介と特性」について要点と要約をまとめました

３つの要点

要点１
ブラウン運動は、平均ゼロ、時間間隔に比例する分散、および独立した増分に特徴付けられる連続時間の確率過程です。
要点２
ブラウン運動のパスは、ジャンプなしで時間の連続関数であり、数学者によってその存在が証明されています。
要点３
ブラウン運動は、どこでも微分不可能である、マルコフ性を持つ、マルチングエールであるなどの興味深い特性を持ち、さまざまな応用分野で価値のあるツールとなっています。

要約

ブラウン運動の概念と特性
このスピーチでは、ブラウン運動の概念について簡単に説明します。ブラウン運動は、連続時間の確率過程であり、ゼロから始まり、独立した標準正規分布の乱数変数が加算されることによって特徴付けられます。この過程には、平均ゼロ、時間間隔に比例する分散、および独立した増分などの特性があります。ブラウン運動は、正規分布で近似される自然現象に類似しているため、さまざまな応用でベンチマークモデルとして使用されます。

ブラウン運動の定義と特性
ブラウン運動は、4つの主要な特性によって定義されます。まず、時間間隔内の過程の増分は、平均ゼロ、分散が間隔の長さに比例する正規分布に従います。次に、過程は独立した増分を持ち、つまり、異なる時間期間間の値の変化は独立したランダム変数です。三つ目に、過程はゼロから始まり、正規化が行われます。最後に、ブラウン運動のパスは、時間の連続関数であり、ジャンプや不連続点はありません。

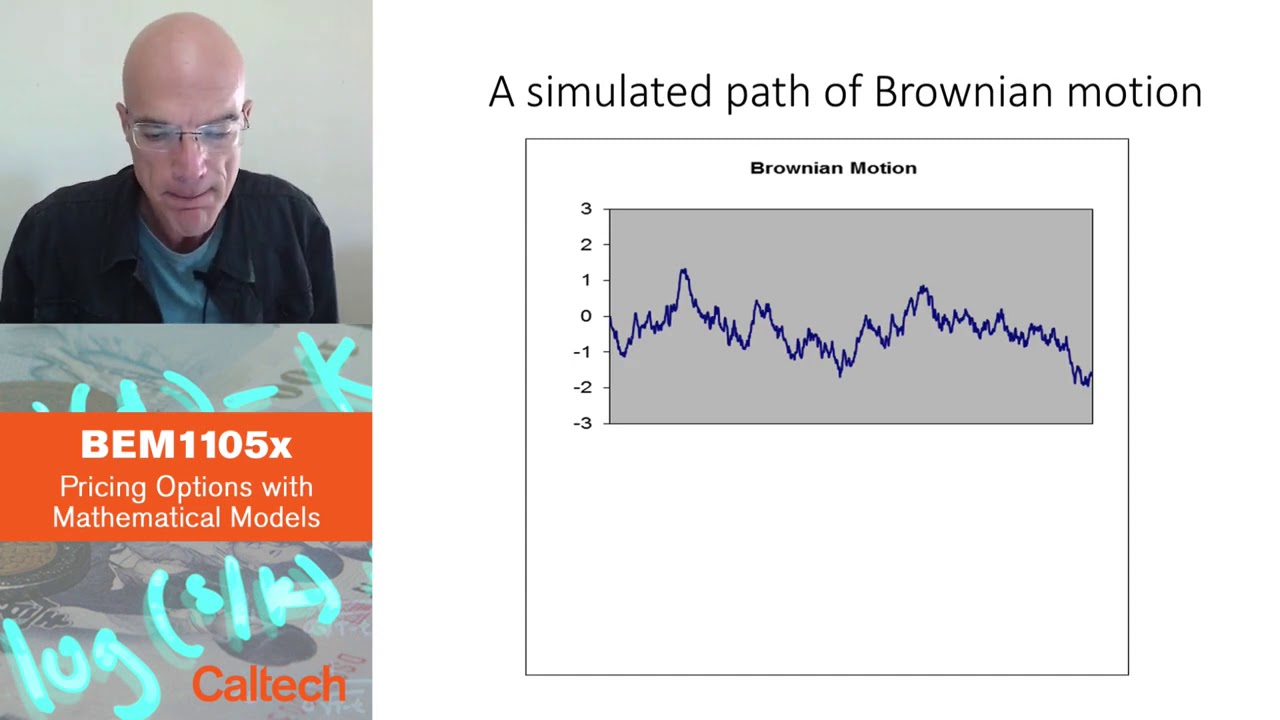
ブラウン運動の存在とシミュレーション
ブラウン運動の存在は、数学者によって証明された数学的な問題でした。証明は困難ですが、ブラウン運動の定義された特性を持つプロセスが存在することが確立されています。さらに、Excelのシミュレーションを使用してブラウン運動のパスを視覚化することができます。各シミュレーションは異なるパスを示しますが、すべてゼロ周りの特徴的な振動と不規則な動きを示します。

ブラウン運動の追加的な特性と応用
ブラウン運動には興味深い特性があります。たとえば、そのパスはどこでも微分可能ではなく、任意の点で接線を定義することはできません。この不規則性は、ブラウン運動に関する導関数の計算や積分を行う際に課題を提起します。しかし、ブラウン運動はマルコフ過程であり、プロセスの将来の値は現在の値にのみ依存し、過去には依存しません。さらに、ブラウン運動はマルチングエールであり、将来の値の最良の予測子は現在の値です。これらの特性により、ブラウン運動は金融や確率論などのさまざまな分野で基本的なツールとなっています。

▼今回の動画