オプションのカレンダースプレッドで曲線状のペイオフを作成する方法
カリフォルニア工科大学のYoutube動画「オプションのカレンダースプレッドで曲線状のペイオフを作成する方法」について要点と要約をまとめました

3つの要点
- 要点1
カレンダースプレッドは曲線状のペイオフを作成するための方法です。 - 要点2
バタフライスプレッドや他のペイオフの形も利用できます。 - 要点3
ほとんどの株価関数は、さまざまな行使価格のコールオプションを使用して作成することができます。

要約
カレンダースプレッドとは
カレンダースプレッドは、異なる満期日のオプションを取引することを意味します。つまり、満期日がp1のコールオプションを売り、より長い満期日のコールオプションを買うことです。株価の関数としてのコールオプションの価値は、滑らかで凸な関数であり、曲線状のペイオフが可能です。
バタフライスプレッドと他のペイオフの形
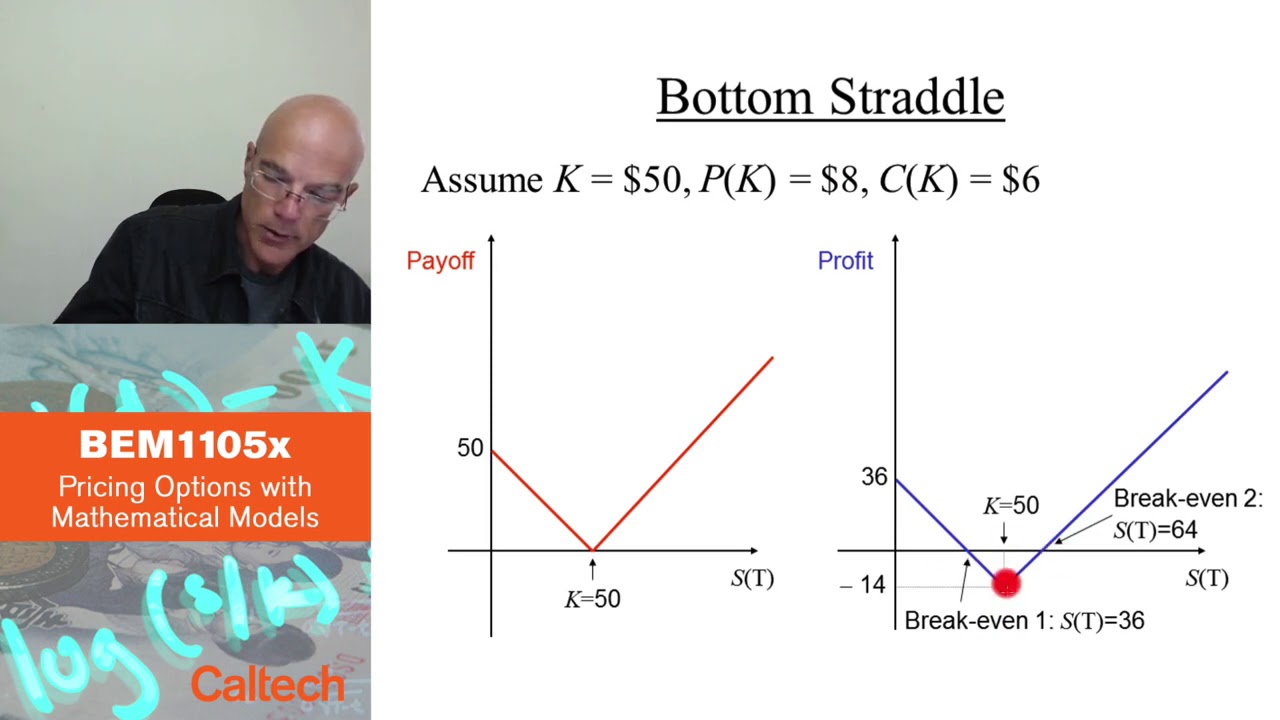
バタフライスプレッドは、満期日が1つのショートプットとショートコールと、より長い満期日のロングコールを組み合わせることで作成することができます。他のペイオフの形としては、ボトムストラドルやボトムストラングルなどがあります。これらは、バニラオプションの静的ポジションを使用して作成することができます。
任意のペイオフを作成する定理
理想化された仮定の下では、ほとんどの株価関数は、さまざまな行使価格のコールオプションを使用して作成することができます。満期時の関数の値は、現金、株のポジション、および異なる行使価格のコールオプションの合計の組み合わせによって近似することができます。
定理の証明
定理の証明には、関数の2階導関数を行使価格に関して積分し、部分積分を使用します。これにより、2階導関数の積分が上限と下限で評価されることがわかり、定理の妥当性が確認されます。
▼今回の動画
編集後記
▼ライターの学び
オプション取引において、異なるオプション戦略を組み合わせることで、さまざまなペイオフ形状を作成することができることを学びました。

▼今日からやってみよう
今日から、異なるオプション戦略を試してみることで、自分自身の投資戦略に多様性をもたらすことができます。